📘 قراءة كتاب المجموعات في البرولوج برامج جاهزة التنفيذ أونلاين


مجموعة من البرامج المحلولة بلغة البرولوج قسم المجموعات والقوائم
تأليف: أ. وائل قاسم سطيح
المجموعات (القوائم)
المجموعة عبارة عن سلسلة من العناصر مرتبة وغير مرتبة وطولها غير محدد ويمكن ان تكون هذه العناصر من أي نوع من الأنواع المعرفة في type بلغة برولوج ويمكن كذلك ان تكون في نفس المجموعة انواع مختلفة فقد تحتوي المجموعة على اعداد صحيحة و أعداد حقيقية و ثوابت وحقائق و مجموعات اخرى وغيره ويفصل بين عناصر المجموعة (الفاصلة) وتبدأ المجموعة بقوس مربع وتنتهي بقوس مربع [] ولتسهيل التعامل مع المجموعة فانه يتم تقسيم المجموعة الى قسمين هما Tail ,Head ويتم الفصل بينهما بالرمز "|"
أقسام المجموعة
List=[H|T]
فهذا يعني ان h هو اول عنصر (Head) وT هو الذيل (Tail) أي بقية عناصر المجموعة فاذا كانت المجموعة كالاتي
List=[1,2,3,4]
فان list=[H|T] عبارة عن H=1 وT=[2,3,4]
اذا كانت المجموعة [1] list= فان H=1 وT=[]
اذا كانت المجموعة list=[1,2,3] فان list=[H1,H2|T] H1=1 ,H2=2 , ,T=[3]
*المساواة والتطابق في المجموعات
• [A,B] =[1,2] => B=2 ,A=1
• [A|B]=[1,2,3] => B=[2,3] , A=1
• ['wael']=[H|T] => T=[] ,H= wael
• [A,'b']= 'a',B => B=b , A=a
• [2,B]=[3,A] Erore لان(2 <> 3)
تعريف المجموعة او القائمة : يتم تعريف المجموعة في domains نفس التعريف للبرامج السابقة ولكن مايميز القائمة هو اضافة العلامة ستار للنوع من اجل ان يخبر المترجم بان المتغير من نوع قائمة مثل
D=symbol*
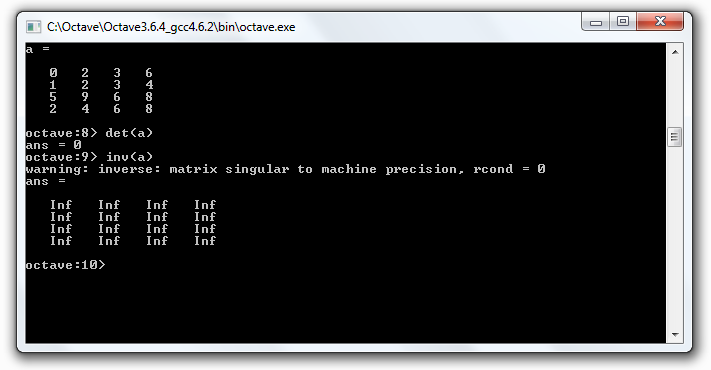
كانت المفارقة عندما جربت تلك المصفوفة على برنامج Octave ، فأعطى النتيجة بالشكل الصحيح بدون عمليات التقريب (Det=0)، كما نلاحظ في الصورة :
المجموعات في البرولوج برامج جاهزة التنفيذ
تعلم لغة البرولوج
prolog list examples
prolog examples
برولوج عملي
نظام خبير بلغة برولوج
تعلم لغة برولوج pdf
تحميل برنامج prolog
برامج مكتوبة بلغة برولوج
تحميل وقراءة أولاين مباشر بدون روابط كتاب المجموعات في البرولوج برامج جاهزة التنفيذ pdf
حجم الكتاب عند التحميل : 688 كيلوبايت .
نوع الكتاب : ppt.
عداد القراءة:
اذا اعجبك الكتاب فضلاً اضغط على أعجبني و يمكنك تحميله من هنا:

شكرًا لمساهمتكم
شكراً لمساهمتكم معنا في الإرتقاء بمستوى المكتبة ، يمكنكم االتبليغ عن اخطاء او سوء اختيار للكتب وتصنيفها ومحتواها ، أو كتاب يُمنع نشره ، او محمي بحقوق طبع ونشر ، فضلاً قم بالتبليغ عن الكتاب المُخالف:
 قبل تحميل الكتاب ..
قبل تحميل الكتاب ..
يجب ان يتوفر لديكم برنامج تشغيل وقراءة ملفات ppt
يمكن تحميلة من هنا 'http://www.microsoftstore.com/store/msmea/ar_EG/pdp/Office-365-Personal/productID.299498600'

 منصّة المكتبة
منصّة المكتبة